Cómo corregir errores numéricos en Ansys para resultados precisos

En el campo de la ingeniería y la simulación por ordenador, Ansys es uno de los programas más utilizados para el análisis y diseño de estructuras y sistemas. Sin embargo, en ocasiones puede presentar errores numéricos que afectan la precisión de los resultados. Estos errores pueden deberse a diversos factores, como la discretización de la geometría, la elección de los parámetros de simulación o el propio algoritmo utilizado por el programa.

Daremos algunos consejos y técnicas para corregir estos errores y obtener resultados más precisos en Ansys. Exploraremos diferentes aspectos, como la definición adecuada de las condiciones de contorno, la elección de elementos finitos apropiados, la adaptación de los parámetros de la simulación y la verificación de la convergencia de los resultados. Además, también discutiremos la importancia de realizar validaciones experimentales y utilizar métodos de verificación independientes para asegurar la calidad de los resultados obtenidos.

Cuáles son los errores numéricos más comunes que se presentan en Ansys y cómo afectan los resultados

En el mundo de la simulación numérica, Ansys es una herramienta ampliamente utilizada para el análisis de ingeniería. Sin embargo, como cualquier software, Ansys no está exento de errores numéricos que pueden afectar la precisión de los resultados obtenidos. Es crucial entender cuáles son estos errores y cómo pueden impactar en nuestros análisis.

Uno de los errores más comunes es el error de redondeo, que se produce cuando los números son aproximados a una cantidad finita de dígitos. Esto puede causar problemas en cálculos que involucran operaciones matemáticas complejas o cuando se trabaja con números muy pequeños o muy grandes.

Otro error frecuente es el error de truncamiento, que ocurre cuando se aproxima un valor real por un número finito de dígitos sin tener en cuenta los dígitos que se encuentran más allá de la precisión seleccionada. Esto puede llevar a resultados inexactos y a la acumulación de errores a medida que se realizan más cálculos.

Además, la discretización del dominio también puede introducir errores numéricos. Los modelos y las mallas utilizadas en Ansys para representar sistemas físicos reales son discretizaciones aproximadas, lo que implica que los resultados obtenidos pueden diferir de los resultados teóricos o experimentales.

Otro error notable es el error de aproximación, que se produce cuando se utiliza una aproximación para simplificar una ecuación o un procedimiento. Aunque estas aproximaciones son necesarias para realizar cálculos complejos de manera eficiente, también pueden introducir errores significativos en los resultados finales.

Es importante destacar que estos errores numéricos pueden acumularse y amplificarse a medida que se realizan más cálculos o se propagan a través de las etapas de un análisis. Por lo tanto, es crucial tomar medidas para minimizar y corregir estos errores con el fin de obtener resultados más precisos y confiables.

Existen métodos o técnicas específicas para corregir errores numéricos en Ansys

Al utilizar Ansys para realizar análisis numéricos, es común encontrarse con errores que pueden afectar la precisión de los resultados. Estos errores pueden surgir debido a diversas razones, como la discretización de mallas, la selección inapropiada de elementos finitos o incluso la manipulación incorrecta de las condiciones de contorno.

Para corregir o minimizar estos errores, es importante aplicar métodos o técnicas específicas que permitan mejorar la precisión de los resultados obtenidos en Ansys. A continuación, se presentarán algunos de estos métodos y técnicas:

1. Refinamiento de malla:

Uno de los métodos más utilizados para corregir errores numéricos en Ansys es el refinamiento de malla. Este proceso consiste en dividir la malla en elementos más pequeños y más cercanos entre sí, lo que proporciona una representación más precisa del dominio del problema. Al aumentar la densidad de la malla, se reduce la propagación de errores numéricos y se mejora la precisión de los resultados.

2. Selección adecuada de elementos finitos:

La elección de los elementos finitos adecuados es crucial para obtener resultados precisos en Ansys. Es importante evaluar detenidamente las características del problema y seleccionar elementos finitos que sean capaces de modelar con precisión el comportamiento del sistema. Al utilizar elementos finitos inapropiados, es posible que se introduzcan errores numéricos significativos, lo que afectará la precisión de los resultados obtenidos.

3. Verificación de las condiciones de contorno:

Las condiciones de contorno desempeñan un papel fundamental en la precisión de los resultados obtenidos en Ansys. Es importante verificar que las condiciones de contorno se establezcan de manera correcta y precisa. Cualquier error en la especificación de las condiciones de contorno puede tener un impacto significativo en los resultados obtenidos. Es recomendable revisar cuidadosamente las condiciones de contorno antes de ejecutar un análisis en Ansys.

4. Uso de técnicas de convergencia:

Las técnicas de convergencia son útiles para corregir errores numéricos en Ansys. Estas técnicas consisten en realizar iteraciones sucesivas en las que se ajustan los parámetros del análisis hasta que los resultados convergen a un valor estable. Al utilizar técnicas de convergencia adecuadas, es posible obtener resultados más precisos y reducir los errores numéricos en Ansys.

5. Validación de resultados:

Para verificar la precisión de los resultados obtenidos en Ansys, es importante realizar comparaciones con datos experimentales o resultados analíticos conocidos. La validación de resultados es fundamental para asegurarse de que los errores numéricos se mantengan dentro de un rango aceptable y que los resultados obtenidos sean consistentes y confiables.

Corregir errores numéricos en Ansys requiere la aplicación de métodos y técnicas específicas que permitan mejorar la precisión de los resultados. El refinamiento de malla, la selección adecuada de elementos finitos, la verificación de las condiciones de contorno, el uso de técnicas de convergencia y la validación de resultados son algunas de estas técnicas que pueden contribuir a obtener resultados más precisos y confiables en Ansys.

Cuál es la importancia de corregir los errores numéricos en Ansys para obtener resultados precisos

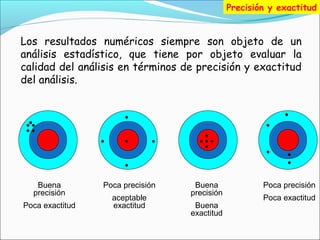
Corregir los errores numéricos en Ansys es crucial para obtener resultados precisos en el análisis de ingeniería. Estos errores pueden surgir debido a la naturaleza discreta de las computadoras y los algoritmos utilizados en Ansys. Si no se corrigen, estos errores pueden afectar significativamente los resultados del análisis y llevar a conclusiones incorrectas. Por lo tanto, es fundamental comprender cómo identificar y corregir estos errores para garantizar la precisión de los resultados en Ansys.

Existen varias fuentes de errores numéricos en Ansys, como la precisión finita de los números de punto flotante y la convergencia del método numérico utilizado. Estos errores pueden acumularse a lo largo de la simulación y provocar desviaciones significativas en los resultados. Además, los errores numéricos también pueden surgir debido a la discretización de los dominios de análisis, como en el caso de elementos finitos.

Identificando errores numéricos en Ansys

Antes de poder corregir los errores numéricos en Ansys, es importante poder identificarlos adecuadamente. Esto puede hacerse mediante el análisis de los resultados obtenidos y comparándolos con soluciones analíticas o resultados esperados. Si hay una discrepancia significativa entre los resultados obtenidos y los esperados, es probable que exista un error numérico.

Además, es útil realizar un análisis de sensibilidad para determinar cómo los cambios en los parámetros de entrada afectan los resultados. Si pequeños cambios en los parámetros de entrada producen cambios significativos en los resultados, esto puede indicar la presencia de errores numéricos.

Cómo corregir errores numéricos en Ansys

Una vez que se han identificado los errores numéricos en Ansys, existen varias técnicas que se pueden utilizar para corregirlos y obtener resultados más precisos. Una de las técnicas más comunes es refinar la malla o la discretización del dominio de análisis. Esto implica dividir los elementos finitos en regiones más pequeñas para mejorar la precisión de los cálculos.

Otra técnica importante es ajustar los parámetros de convergencia utilizados en los solucionadores numéricos de Ansys. Estos parámetros controlan la precisión y la convergencia de los cálculos y pueden ajustarse para reducir los errores numéricos. Sin embargo, es importante tener en cuenta que ajustar los parámetros de convergencia puede aumentar el tiempo de cálculo, por lo que es necesario encontrar un equilibrio entre la precisión y la eficiencia.

Además, es recomendable utilizar elementos finitos de mayor orden, como elementos cuadráticos o cúbicos, en lugar de elementos lineales estándar. Estos elementos de orden superior pueden proporcionar una mejor aproximación de los campos físicos y reducir los errores numéricos.

Corregir los errores numéricos en Ansys es esencial para obtener resultados precisos en el análisis de ingeniería. Mediante la identificación adecuada de los errores y el uso de técnicas de corrección, como la refinación de la malla y el ajuste de los parámetros de convergencia, se puede garantizar la precisión de los resultados. Al seguir estos pasos, los ingenieros pueden tener confianza en los resultados obtenidos a través de Ansys y tomar decisiones informadas en sus proyectos de ingeniería.

Cómo se pueden identificar los errores numéricos en los resultados de Ansys

La simulación numérica es una valiosa herramienta en ingeniería para predecir el comportamiento de sistemas complejos. Sin embargo, es común encontrar errores numéricos en los resultados obtenidos a través de software como Ansys. Estos errores pueden ser causados por diversos factores, como la discretización de la geometría, la elección inapropiada de elementos finitos o la falta de precisión en los cálculos.

Para identificar errores numéricos en los resultados de Ansys, es esencial realizar un análisis crítico de los mismos. Una forma de hacerlo es comparar los resultados obtenidos con los valores esperados. Si existe una discrepancia significativa, es probable que haya un error numérico. Además, es importante tener en cuenta las unidades utilizadas y las condiciones de contorno aplicadas, ya que cualquier error en estos aspectos puede afectar la precisión de los resultados.

Otro método para identificar errores numéricos es realizar una convergencia de la solución. Esto implica realizar simulaciones con diferentes tamaños de malla o refinamientos, y comparar los resultados obtenidos. Si los resultados no convergen hacia un valor estable, es indicativo de la presencia de errores numéricos. Además, se pueden utilizar técnicas de post-procesamiento, como la interpolación de datos o el suavizado de resultados, para identificar posibles errores o inconsistencias en los resultados numéricos.

Es importante destacar que los errores numéricos no siempre son evitables, pero se pueden minimizar mediante una cuidadosa selección de parámetros de simulación y una verificación constante de los resultados obtenidos. Además, es recomendable consultar la documentación de Ansys y buscar la orientación de expertos en el área para obtener resultados más precisos y confiables.

Hay diferencias en la forma de corregir errores numéricos dependiendo del tipo de análisis realizado en Ansys

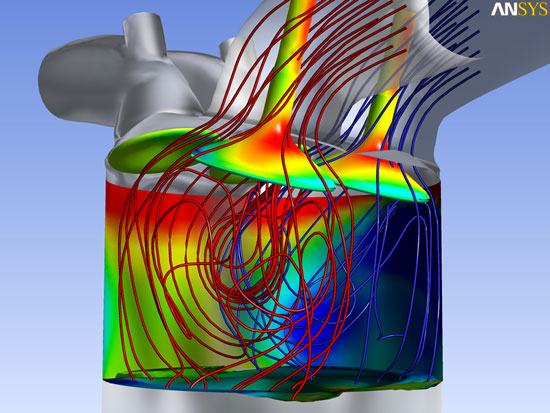
Cuando trabajamos con Ansys, es común enfrentarnos a errores numéricos que pueden afectar la precisión de nuestros resultados. Estos errores pueden ocurrir debido a diversos factores, como la discretización de la geometría, los modelos matemáticos utilizados o las condiciones de contorno definidas. Para obtener resultados precisos, es importante ser consciente de estos errores y saber cómo corregirlos.

Corrección de errores en análisis estructurales

En los análisis estructurales, uno de los errores más comunes es el error de convergencia. Este error ocurre cuando la solución numérica no converge correctamente y se obtienen resultados incorrectos o inestables. Para corregir este error, se pueden tomar varias medidas. Una de ellas es ajustar los parámetros de convergencia en Ansys, como el criterio de convergencia o el número máximo de iteraciones. Otra opción es mejorar la discretización de la geometría utilizando elementos más refinados.

Otro tipo de error que puede ocurrir en análisis estructurales es el error de rigidez. Este error se produce cuando las propiedades mecánicas de los materiales no se modelan de manera precisa. Para corregir este error, es necesario revisar y ajustar los valores de los módulos de elasticidad, coeficientes de Poisson y demás propiedades materiales utilizadas en el análisis.

Corrección de errores en análisis de flujo de fluidos

En los análisis de flujo de fluidos, uno de los errores más comunes es el error de convergencia en el campo de velocidades. Este error puede ocurrir cuando las condiciones de contorno no se definen correctamente o cuando los parámetros de convergencia no están adecuadamente ajustados. Para corregir este error, se recomienda revisar y ajustar las condiciones de contorno, así como los parámetros de convergencia, como el criterio de convergencia y la tolerancia.

Otro tipo de error que puede ocurrir en análisis de flujo de fluidos es el error de discretización. Este error se produce cuando la malla utilizada para discretizar la geometría no es lo suficientemente fina, lo que lleva a una aproximación imprecisa de los resultados. Para corregir este error, se deben utilizar mallas más refinadas o técnicas de refinamiento adaptativo de mallas.

Corrección de errores en análisis térmicos

En los análisis térmicos, uno de los errores más comunes es el error de convergencia en la distribución de temperaturas. Este error puede ocurrir cuando las condiciones de contorno no se definen adecuadamente o cuando los parámetros de convergencia no están correctamente ajustados. Para corregir este error, se recomienda revisar y ajustar las condiciones de contorno, así como los parámetros de convergencia, como el criterio de convergencia y la tolerancia.

Otro tipo de error que puede ocurrir en análisis térmicos es el error de discretización. Este error ocurre cuando la malla utilizada para discretizar la geometría no es lo suficientemente fina, lo que lleva a una aproximación imprecisa de los resultados de temperatura. Para corregir este error, se deben utilizar mallas más refinadas o técnicas de refinamiento adaptativo de mallas.

Qué precauciones se deben tomar al corregir errores numéricos en Ansys para evitar la introducción de nuevos errores

Cuando se trabaja con Ansys, es común encontrarse con errores numéricos que pueden afectar la precisión de los resultados. Sin embargo, corregir estos errores no es tan sencillo como parece. Es importante tomar precauciones para evitar la introducción de nuevos errores en el proceso.

Una de las precauciones más importantes es entender la causa raíz del error. Esto requiere un análisis exhaustivo de los datos y del modelo utilizado. Es posible que el error se deba a una mala discretización de la geometría, una mala definición de las condiciones de frontera o una elección inadecuada de los parámetros del análisis.

Una vez identificada la causa del error, se deben tomar medidas correctivas. Esto puede implicar la modificación de la geometría, la revisión de las condiciones de frontera o la recalibración de los parámetros del análisis. Es importante tener en cuenta que cualquier cambio realizado debe estar respaldado por una justificación técnica sólida.

Otro aspecto crucial es verificar la corrección de los errores introducidos. Esto implica realizar simulaciones adicionales para comparar los resultados obtenidos antes y después de la corrección. Es importante asegurarse de que los resultados corregidos sean consistentes y estén dentro de los límites de error aceptables.

Además, es fundamental documentar todo el proceso de corrección de errores. Esto incluye registrar las modificaciones realizadas en el modelo, las justificaciones técnicas correspondientes y los resultados de las simulaciones de verificación. Esta documentación será útil para futuros análisis y para garantizar la reproducibilidad de los resultados.

Corregir errores numéricos en Ansys requiere de precauciones para evitar la introducción de nuevos errores. Esto incluye comprender la causa raíz del error, tomar medidas correctivas respaldadas por justificaciones técnicas, verificar la corrección de los errores y documentar todo el proceso. Siguiendo estas precauciones, se pueden obtener resultados más precisos y confiables en el análisis con Ansys.

Existen herramientas o recursos adicionales que se puedan utilizar para corregir errores numéricos en Ansys

¡Claro que sí! Ansys es una poderosa herramienta de simulación, pero en ocasiones los resultados pueden contener errores numéricos. Afortunadamente, existen diversas herramientas y recursos que podemos utilizar para corregir estos errores y obtener resultados más precisos.

1. Verificar las unidades utilizadas

Es importante asegurarnos de que todas las unidades utilizadas en nuestro modelo sean consistentes. Ansys suele utilizar el sistema internacional de unidades (SI), por lo que es recomendable trabajar en este sistema para evitar posibles errores de conversión.

2. Refinar la malla

Uno de los principales factores que pueden influir en la precisión de los resultados es la malla utilizada en la simulación. Si la malla es muy gruesa, los resultados pueden ser aproximados. Por ello, es recomendable refinar la malla en zonas críticas o de interés para obtener resultados más precisos.

3. Aumentar el número de elementos

En algunos casos, aumentar el número de elementos en nuestro modelo puede ayudar a obtener resultados más precisos. Esto se aplica especialmente a problemas que implican gradientes de temperatura o esfuerzos muy localizados. Aumentar el número de elementos permitirá una mejor representación de estas variaciones y, por lo tanto, resultados más precisos.

4. Utilizar métodos de convergencia

Ansys ofrece varios métodos de convergencia que nos permiten obtener resultados más precisos. Entre ellos se encuentran los métodos de refinamiento adaptativo, que ajustan automáticamente la malla en función de los resultados obtenidos, y los métodos iterativos, que permiten alcanzar una solución más precisa a través de múltiples iteraciones.

5. Verificar las condiciones de contorno

Es importante revisar las condiciones de contorno utilizadas en nuestro modelo. Un error en las condiciones de contorno puede derivar en resultados incorrectos o imprecisos. Verificar que todas las condiciones de contorno estén correctamente definidas y aplicadas es fundamental para obtener resultados precisos.

6. Validar los resultados

Para corregir errores numéricos en Ansys, es importante validar los resultados obtenidos. Esto implica comparar los resultados simulados con datos experimentales o soluciones analíticas conocidas. Si los resultados no concuerdan, es posible que existan errores numéricos que debamos corregir.

7. Actualizar Ansys

Por último, es recomendable mantener nuestra versión de Ansys actualizada. Las actualizaciones suelen incluir mejoras y correcciones que pueden ayudar a corregir errores numéricos y obtener resultados más precisos. Verificar periódicamente si hay actualizaciones disponibles y aplicarlas en nuestro sistema es una buena práctica para mejorar la precisión de nuestros resultados.

Ahora que conoces estas herramientas y recursos adicionales, podrás corregir errores numéricos en Ansys y obtener resultados más precisos en tus simulaciones. Recuerda siempre verificar las unidades, refinar la malla, aumentar el número de elementos, utilizar métodos de convergencia, verificar las condiciones de contorno, validar los resultados y mantener Ansys actualizado. ¡Adelante, mejora tus resultados y alcanza la precisión que necesitas!

Es posible minimizar el impacto de los errores numéricos en Ansys sin corregirlos por completo

Al trabajar con simulaciones numéricas en Ansys, es común encontrar errores numéricos que pueden afectar la precisión de los resultados. Estos errores pueden ser causados por diversas razones, como la discretización de la geometría, la elección de los parámetros de simulación o incluso la precisión de la computadora en la que se está ejecutando el software.

¿Por qué corregir los errores numéricos en Ansys?

Corregir los errores numéricos en Ansys es fundamental para obtener resultados precisos y confiables. Estos errores pueden introducir inexactitudes en los cálculos, lo que podría llevar a decisiones erróneas o a la interpretación incorrecta de los resultados. Además, la precisión de los resultados es especialmente importante en casos donde se toman decisiones críticas o se realizan diseños basados en los resultados obtenidos.

Posibles estrategias para corregir los errores numéricos en Ansys

Para corregir los errores numéricos en Ansys, es necesario tener en cuenta varias estrategias. En primer lugar, es importante realizar una buena discretización de la geometría, utilizando elementos de malla adecuados y refinando la malla en las zonas de mayor interés. Además, es crucial seleccionar los parámetros de simulación de manera adecuada, considerando la magnitud de los fenómenos físicos que se están modelando.

Otra estrategia para corregir los errores numéricos en Ansys es utilizar técnicas de refinamiento de malla adaptativo. Estas técnicas permiten refinar automáticamente la malla en las zonas donde se detectan mayores errores numéricos, mejorando así la precisión de los resultados. Además, es posible utilizar métodos de interpolación o ajuste de curvas para mejorar la precisión de los resultados obtenidos.

Explosión en la generación de resultados numéricos en Ansys

La explosión en la generación de resultados numéricos en Ansys se refiere a la generación de una gran cantidad de resultados en un corto período de tiempo. Esto se logra utilizando técnicas de paralelización y utilizando la potencia de computación de múltiples núcleos o incluso de múltiples máquinas. Esta explosión en la generación de resultados permite obtener una visión más completa y detallada del problema que se está resolviendo, mejorando así la precisión de los resultados obtenidos.

Corregir los errores numéricos en Ansys es fundamental para obtener resultados precisos y confiables. Para lograrlo, es necesario considerar diversas estrategias, como la buena discretización de la geometría, la selección adecuada de los parámetros de simulación y el uso de técnicas de refinamiento de malla adaptativo. Además, la explosión en la generación de resultados numéricos en Ansys permite obtener una visión más completa y detallada del problema, mejorando así la precisión de los resultados obtenidos.

Cuál es la influencia de los errores numéricos en la eficiencia del análisis en Ansys

Los errores numéricos son una preocupación común en el análisis realizado con Ansys. Estos errores pueden afectar significativamente la precisión de los resultados obtenidos, lo que a su vez puede tener un impacto en la eficiencia global del análisis.
Los errores numéricos pueden surgir debido a varias razones, como la discretización de los dominios físicos, los errores de redondeo en los cálculos matemáticos y la convergencia inexacta de las iteraciones. Estos errores pueden acumularse a lo largo del análisis y, si no se corrigen, pueden llevar a resultados inexactos y poco confiables.

Por lo tanto, es esencial abordar estos errores y corregirlos para obtener resultados precisos y confiables en Ansys.

Identificar y comprender los errores numéricos

El primer paso para corregir los errores numéricos en Ansys es identificarlos y comprender su naturaleza y origen. Esto implica examinar las salidas del análisis, como los informes de errores y los gráficos de convergencia, para identificar cualquier comportamiento anómalo o indicio de errores numéricos.

Una vez identificados, es necesario comprender la causa raíz de estos errores numéricos. Por ejemplo, los errores de redondeo pueden surgir debido a limitaciones en la precisión de la aritmética de punto flotante utilizada por el sistema. Comprender la causa raíz permitirá tomar las medidas adecuadas para corregir o mitigar estos errores.

Optimizar la discretización

Una de las principales fuentes de errores numéricos en Ansys es la discretización de los dominios físicos. Esta discretización implica dividir el dominio en elementos finitos más pequeños para simplificar los cálculos. Sin embargo, si la discretización no es adecuada, puede dar lugar a errores numéricos significativos.

Para corregir estos errores, es fundamental optimizar la discretización. Esto implica ajustar los parámetros de discretización, como el tamaño de los elementos y el número de elementos en la malla, para obtener una mayor precisión en los resultados.

Además, es importante realizar un análisis de sensibilidad para evaluar el impacto de los errores de discretización en los resultados y determinar la resolución óptima que proporciona resultados precisos y confiables.

Implementar métodos de convergencia robustos

La convergencia inexacta de las iteraciones es otra fuente común de errores numéricos en Ansys. Este problema puede surgir cuando los criterios de convergencia no se establecen correctamente o cuando hay dificultades en la solución del sistema de ecuaciones resultante de las iteraciones.

Para corregir estos errores, es necesario implementar métodos de convergencia robustos. Esto implica ajustar los criterios de convergencia, como los valores de tolerancia y los límites de iteraciones, para garantizar una convergencia precisa y confiable. Además, es importante considerar la elección del método de solución más adecuado para el problema en cuestión.

Además de los métodos de convergencia, también es beneficioso utilizar técnicas de precondicionamiento para mejorar la eficiencia y precisión del análisis. Estas técnicas implican la manipulación de las ecuaciones del sistema para reducir la condición de mal acondicionamiento y mejorar la convergencia.

Verificar los resultados corregidos

Una vez implementadas las correcciones para los errores numéricos en Ansys, es fundamental verificar los resultados para asegurarse de que sean precisos y confiables.

Esto implica realizar pruebas de validación y comparar los resultados corregidos con casos de referencia o datos experimentales. Si los resultados corregidos se acercan a los valores de referencia o se ajustan a los datos experimentales dentro de un margen aceptable de error, se puede considerar que los errores numéricos han sido corregidos de manera efectiva.

En caso contrario, es necesario revisar las correcciones realizadas y realizar ajustes adicionales para lograr resultados precisos y confiables.

Corregir los errores numéricos en Ansys es esencial para obtener resultados precisos y confiables en el análisis. Esto implica identificar y comprender los errores, optimizar la discretización, implementar métodos de convergencia robustos y verificar los resultados corregidos. Al abordar estos errores de manera efectiva, se puede mejorar la eficiencia y precisión global del análisis en Ansys.

Qué tan frecuente es encontrar errores numéricos en los resultados de Ansys y cómo se pueden evitar en futuros análisis

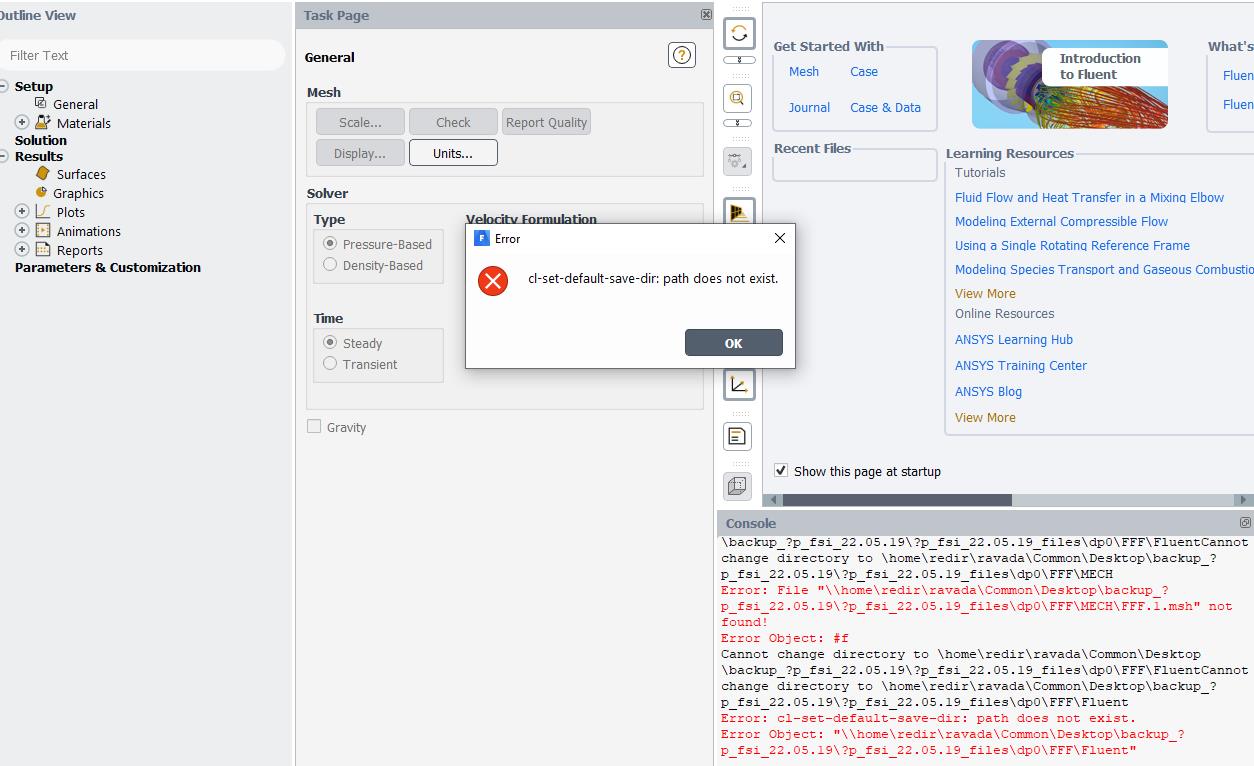
Los errores numéricos en los resultados de Ansys son algo común y pueden afectar significativamente la precisión de los análisis. Estos errores pueden ocurrir debido a varios factores, como la elección inapropiada de elementos finitos, una malla de elementos de baja calidad o problemas de convergencia. Además, las limitaciones de la capacidad de cálculo de la computadora también pueden contribuir a estos errores.

Para evitar errores numéricos en futuros análisis, es importante seguir algunas prácticas recomendadas. En primer lugar, se recomienda utilizar elementos finitos de alta calidad y garantizar una malla de elementos adecuada. Esto implica la revisión y mejora de la malla para asegurar que los elementos finitos estén correctamente distribuidos y que no haya áreas con una malla demasiado fina o gruesa.

También es crucial verificar la convergencia de los resultados antes de dar por finalizado el análisis. La convergencia se refiere a la estabilidad y consistencia de los resultados a medida que se incrementa el número de iteraciones. Si los resultados no convergen, es necesario ajustar los parámetros de análisis, como el tamaño de paso de tiempo o la tolerancia de convergencia, hasta obtener resultados estables y consistentes.

Errores comunes y cómo corregirlos

• Out of memory error: Este error ocurre cuando el análisis requiere más memoria de la disponible en la computadora. Para solucionarlo, se pueden utilizar técnicas como la subdivisión de la malla en regiones más pequeñas o el uso de métodos de reducción de memoria.
• Singular matrix error: Este erro